2020 Nov P2 Q4

Question 4

$M(-3\,;\,4)$ is the centre of the large circle and a point on the small circle having centre $O(0\,;\,0)$ . From $N(-11\,;\,p)$ , a tangent is drawn to touch the large circle at $T$ with $NT$ is parallel to the $y$ -axis. $NM$ is a tangent to the smaller circle at $M$ with $MOS$ a diameter.

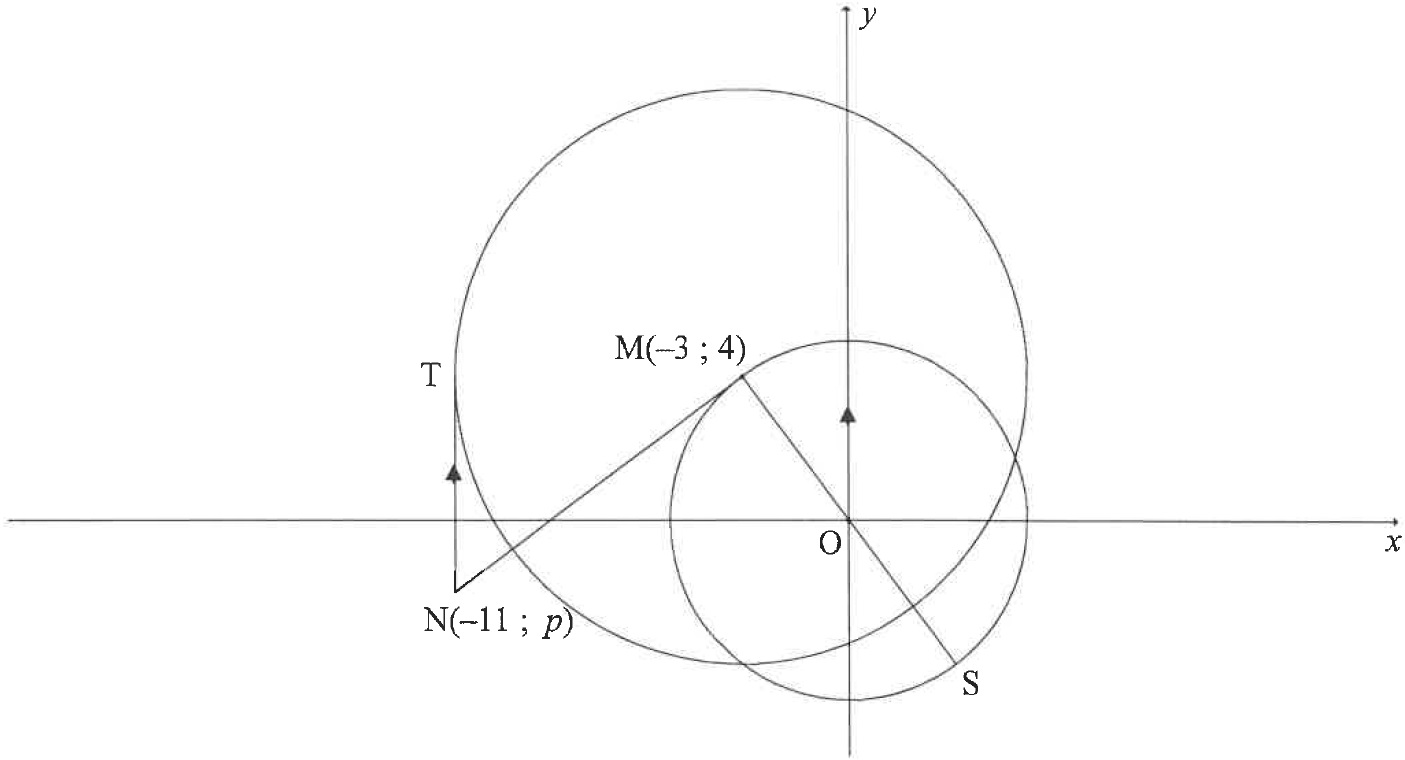$4.1$	Determine the equation of the small circle.	$(2)$
$4.2$	Determine the equation of the circle centred at $M$ in the form $(x-a)^2+(y-b)^2=r^2$	$(3)$
$4.3$	Determine the equation of $NM$ in the form $y=mx+c$	$(4)$
$4.4$	Calculate the length of $SN$ .	$(5)$
$4.5$	If another circle with centre $B(-2\,;\,5)$ and radius $k$ touches the circle centred at $M$ , determine the value(s) of $k$ , correct to ONE decimal place.	$(5)$
		$\textbf{[19]}$