2020 Nov P2 Q3

Question 3

$\Delta TSK$ is drawn. The equation of $ST$ is $y=\frac{\displaystyle 1}{\displaystyle 2}x+6$ and $ST$ cuts the $x$ -axis at $M$ . $W(-4\,;\,4)$ lies on $ST$ and $R$ lies on $SK$ such that $WR$ is parallel to the $y$ -axis. $WK$ cuts the $x$ -axis at $V$ and the $y$ -axis at $P(0\,;\,-4)$ . $KS$ produced cuts the $x$ -axis at $N$ . $T\hat SK=\theta \,$ .

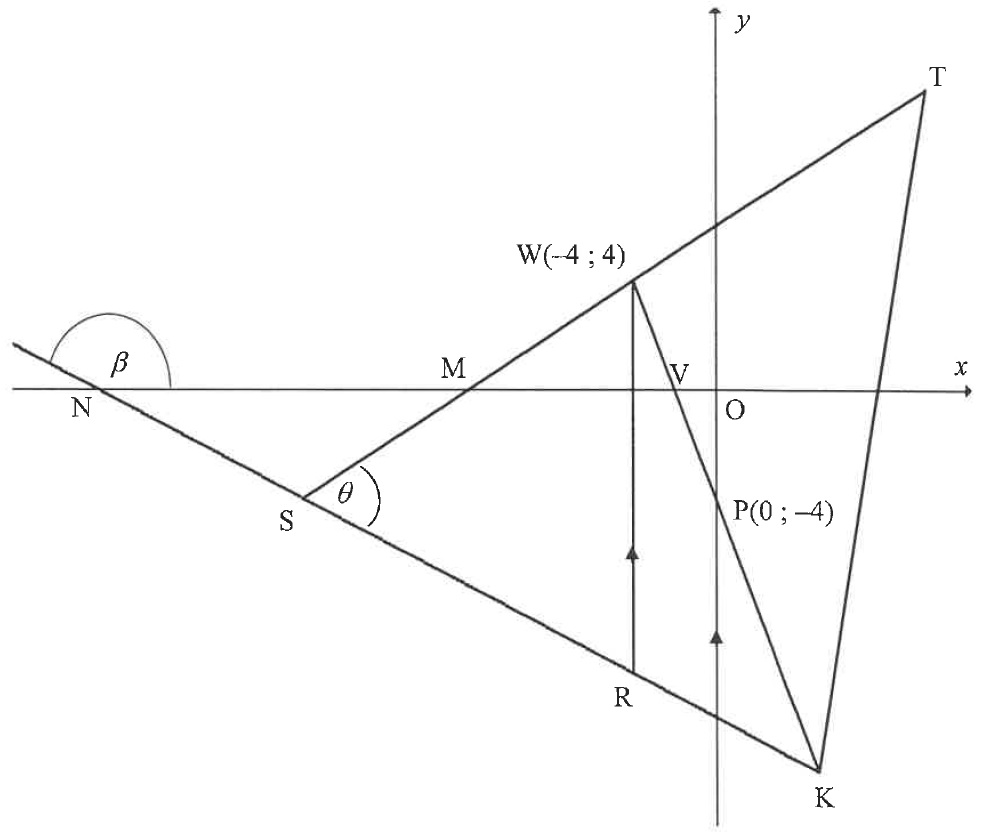$3.1$	Calculate the gradient of $WP$ .	$(2)$
$3.2$	Show that $WP\perp ST$ .	$(2)$
$3.3$	If the equation of $SK$ is given as $5y+2x+60=0$ , calculate the coordinates of $S$ .	$(4)$
$3.4$	Calculate the length of $WR$ .	$(3)$
$3.5$	Calculate the size of $\theta$ .	$(5)$
$3.6$	Let $L$ be a point in the third quadrant such that $SWRL$ , in that order, forms a parallelogram. Calculate the area of $SWRL$ .	$(4)$
		$\textbf{[21]}$