2020 Nov P2 Q10

Written on
November 2020 - Paper 2

Question 1

A Mathematics teacher was curious to establish if her learners' Mathematics marks influenced their Physical Sciences marks. In the table below, the Mathematics and Physical Sciences marks of

15

learners in her class are given as percentages

(\%)

.

$\:$ MATHEMATICS (AS $\%$ )	$26$	$62$	$21$	$33$	$53$	$76$	$32$	$59\:\:$
$\:$ MATHEMATICS (AS $\%$ )	$\:\:43$	$33$	$49$	$51$	$19$	$34$	$85$
$\:$ PHYSICAL SCIENCES (AS $\%$ )	$34$	$67$	$28$	$46$	$65$	$76$	$26$	$73\:\:$
$\:$ PHYSICAL SCIENCES (AS $\%$ )	$\:\:50$	$39$	$57$	$51$	$24$	$41$	$80$

1.1

Determine the equation of the least squares regression line for the data.

(3)

1.2

Draw the least squares regression line on the scatter plot provided in the ANSWER BOOK.

(2)

1.3

Predict the Physical Sciences mark of a learner who achieved

69\%

for Mathematics.

(2)

1.4

Write down the correlation coefficient between the Mathematics and Physical Sciences marks for the data.

(1)

1.5

Comment on the strength of the correlation between the Mathematics and Physical Sciences marks for the data.

(1)

1.6

What trend did the teacher observe between the results of the two subjects?

(1)

\textbf{[10]}

Written on
November 2020 - Paper 2

Question 2

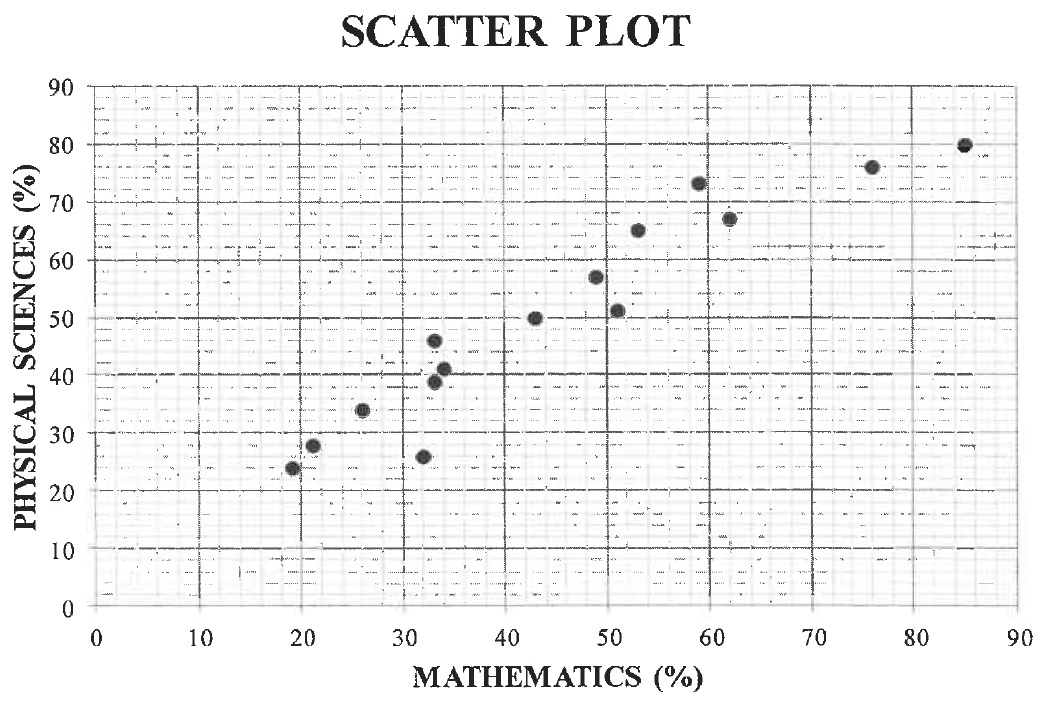
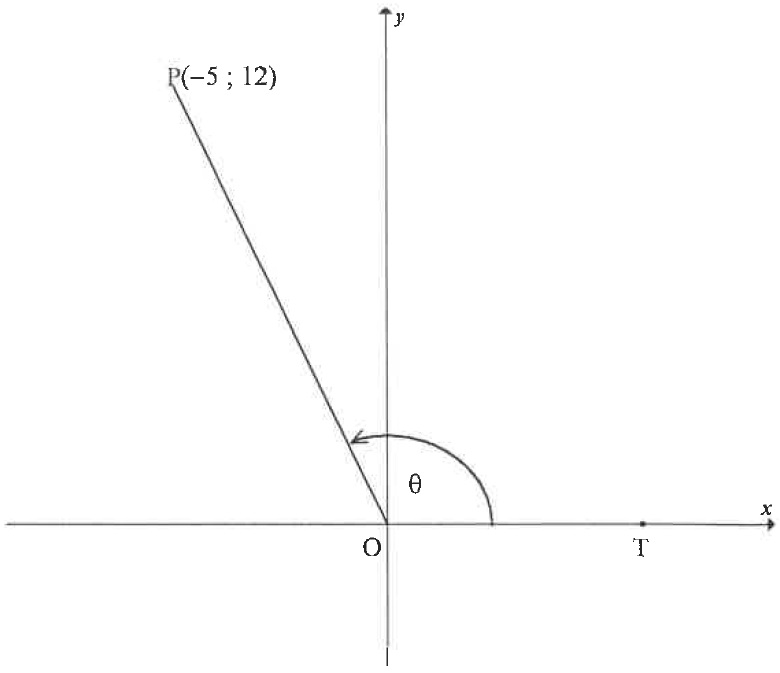
The number of aircraft landing at the King Shaka International Airport and the Port Elizabeth Airport for the period starting in April

2017

and ending in March

2018

, is shown in the double bar graph below.

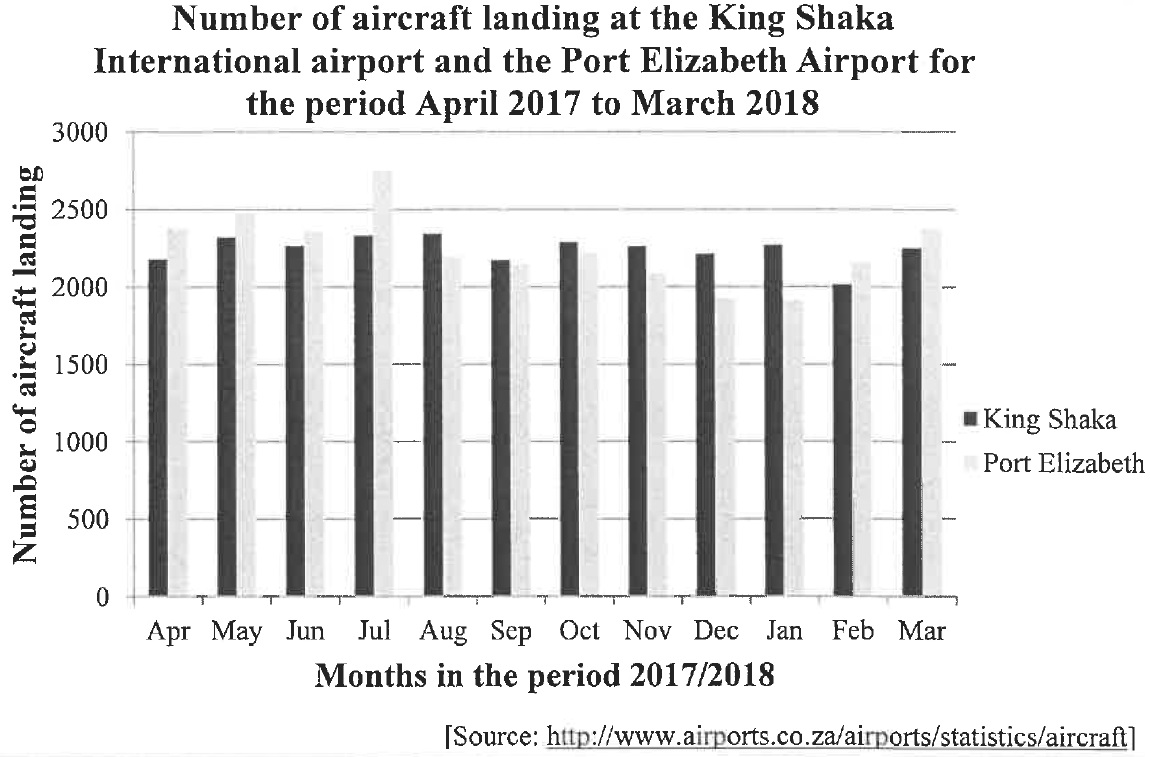2.1

The number of aircraft landing at the Port Elizabeth Airport exceeds the number of aircraft landing at the King Shaka International Airport during some months of the given period. During which month is this difference the greatest?

(1)

2.2

The number of aircraft landing at the King Shaka International Airport during these months are:

$\:\:2\,182$	$2\,323$	$2\,267$	$2\,334$	$2\,346$	$2\,175$
$\:\:2\,293$	$2\,263$	$2\,215$	$2\,271$	$2\,018$	$2\,254$

Calculate the mean for the data.

(2)

2.3

Calculate the standard deviation for the number of aircraft landing at the King Shaka International Airport for the given period.

(2)

2.4

Determine the number of months in which the number of aircraft landing at the King Shaka International Airport were within one standard deviation of the mean.

(3)

2.5

Which ONE of the following statements is CORRECT?

\quad A.

During December and January, there were more landings at the Port Elizabeth Airport than at the King Shaka International Airport.

\quad B.

There was a greater variation in the number of aircraft landing at the King Shaka International Airport than at the Port Elizabeth Airport for the given period.

\quad C.

The standard deviation of the number of landings at the Port Elizabeth Airport will be higher than the standard deviation of the number of landings at the King Shaka International Airport.

(1)

\textbf{[9]}

Written on
November 2020 - Paper 2

Question 3

$\Delta TSK$ is drawn. The equation of $ST$ is $y=\frac{\displaystyle 1}{\displaystyle 2}x+6$ and $ST$ cuts the $x$ -axis at $M$ . $W(-4\,;\,4)$ lies on $ST$ and $R$ lies on $SK$ such that $WR$ is parallel to the $y$ -axis. $WK$ cuts the $x$ -axis at $V$ and the $y$ -axis at $P(0\,;\,-4)$ . $KS$ produced cuts the $x$ -axis at $N$ . $T\hat SK=\theta \,$ .

$3.1$	Calculate the gradient of $WP$ .	$(2)$
$3.2$	Show that $WP\perp ST$ .	$(2)$
$3.3$	If the equation of $SK$ is given as $5y+2x+60=0$ , calculate the coordinates of $S$ .	$(4)$
$3.4$	Calculate the length of $WR$ .	$(3)$
$3.5$	Calculate the size of $\theta$ .	$(5)$
$3.6$	Let $L$ be a point in the third quadrant such that $SWRL$ , in that order, forms a parallelogram. Calculate the area of $SWRL$ .	$(4)$
		$\textbf{[21]}$

Written on
November 2020 - Paper 2

Question 4

$M(-3\,;\,4)$ is the centre of the large circle and a point on the small circle having centre $O(0\,;\,0)$ . From $N(-11\,;\,p)$ , a tangent is drawn to touch the large circle at $T$ with $NT$ is parallel to the $y$ -axis. $NM$ is a tangent to the smaller circle at $M$ with $MOS$ a diameter.

$4.1$	Determine the equation of the small circle.	$(2)$
$4.2$	Determine the equation of the circle centred at $M$ in the form $(x-a)^2+(y-b)^2=r^2$	$(3)$
$4.3$	Determine the equation of $NM$ in the form $y=mx+c$	$(4)$
$4.4$	Calculate the length of $SN$ .	$(5)$
$4.5$	If another circle with centre $B(-2\,;\,5)$ and radius $k$ touches the circle centred at $M$ , determine the value(s) of $k$ , correct to ONE decimal place.	$(5)$
		$\textbf{[19]}$

Written on
November 2020 - Paper 2

Question 5

The graphs of $f(x)=-\frac{\displaystyle 1}{\displaystyle 2}\cos x$ and $g(x)=\sin (x+30^{\circ})$ , for the interval $x\in[0^{\circ}\,;\,180^{\circ}]$ , are drawn below. $A(130,9^{\circ}\,;\,0,33)$ is the approximate point of intersection of the two graphs.

$5.1$	Write down the period of $g$ .	$(1)$
$5.2$	Write down the amplitude of $f$ .	$(1)$
$5.3$	Determine the value of $f(180^{\circ})-g(180^{\circ})$	$(1)$
$5.4$	Use the graphs to determine the values of $x$ , in the interval $x\in[0^{\circ}\,;\,180^{\circ}]$ , for which:
$\quad 5.4.1$	$f(x-10^{\circ})=g(x-10^{\circ})$	$(1)$
$\quad 5.4.2$	$\sqrt{3}\sin x+\cos x \geq 1$	$(4)$
		$\textbf{[8]}$

Written on
November 2020 - Paper 2

Question 6

$6.1$	In the diagram, $P(-5\,;\,12)$ and $T$ lies on the positive $x$ -axis. $P\hat OT=\theta$

Answer the following without using a calculator:
$\quad 6.1.1$	Write down the value of $\tan\theta$	$(1)$
$\quad 6.1.2$	Calculate the value of $\cos\theta$	$(3)$
$\quad 6.1.3$	$S(a\,;\,b)$ is a point in the third quadrant such that $T\hat OS=\theta+90^{\circ}$ and $OS=6,5$ units. Calculate the value of $b$ .	$(4)$
$6.2$	Determine, without using a calculator, the value of the following trigonometric expression: $\frac{\displaystyle \sin{2x}.\cos(-x)+\cos{2x}.\sin(360^{\circ}-x)}{\displaystyle \sin(180^{\circ}+x)}$	$(5)$
$6.3$	Determine the general solution of the following equation: $6\sin^2 x+7\cos{x}-3=0$	$(6)$
$6.4$	Given: $x+\frac{\displaystyle 1}{\displaystyle x}=3\cos{A}$ and $x^2+\frac{\displaystyle 1}{\displaystyle x^2}=2$ Determine the value of $\cos{2A}$ without using a calculator.	$(5)$
		$\textbf{[24]}$

Written on
November 2020 - Paper 2

Question 7

A landscape artist plans to plant flowers within two concentric circles around a vertical light pole $PQ$ . $R$ is a point on the inner circle and $S$ is a point on the outer circle. $R$ , $Q$ and $S$ lie in the same horizontal plane. $RS$ is a pipe used for the irrigation system in the garden. The radius of the inner circle is $r$ units and the radius of the outer circle is $QS$ . The angle of elevation from $S$ to $P$ is $30^{\circ}$ . $R\hat QS=2x$ and $PQ=\sqrt{3}r$

$7.1$	Show that $QS=3r$	$(3)$
$7.2$	Determine, in terms of $r$ , the area of the flower garden.	$(2)$
$7.3$	Show that $RS=r\sqrt{10-6\cos{2x}}$	$(3)$
$7.4$	If $r=10$ metres and $x=56^{\circ}$ , calculate $RS$ .	$(2)$
		$\textbf{[10]}$

Written on
November 2020 - Paper 2

Question 8.1

$8.1$	$O$ is the centre of the circle. $KOM$ bisects chord $LN$ and $M\hat NO=26^{\circ}$ . $K$ and $P$ are points on the circle with $N\hat KP=32^{\circ}$ . $OP$ is drawn.

$\:\: 8.1.1$	Determine, giving reasons, the size of:
$\quad (a)$	$\hat O_2$	$(2)$
$\quad (b)$	$\hat O_1$	$(4)$
$\:\: 8.1.2$	Prove, giving reasons, that $KN$ bisects $O\hat KP$ .	$(3)$
		$\textbf{[9]}$

Written on
November 2020 - Paper 2

Question 8.2

$8.2$	In $\Delta ABC$ , $F$ and $G$ are points on sides $AB$ and $AC$ respectively. $D$ is a point on $GC$ such that $\hat D_1=\hat B$ .

$\quad 8.2.1$	If $AF$ is a tangent to the circle passing through points $F$ , $G$ and $D$ , then prove, giving reasons, that $FG\parallel BC$ .	$(4)$
$\quad 8.2.2$	If it is further given that $\frac{\displaystyle AF}{\displaystyle FB}=\frac{\displaystyle 2}{\displaystyle 5}$ , $AC=2x-6$ and $GC=x+9$ , then calculate the value of $x$ .	$(4)$
		$\textbf{[8]}$

Written on
November 2020 - Paper 2

Question 9.1

$9.1$	In the diagram, $O$ is the centre of the circle. Points $S$ , $T$ and $R$ lie on the circle. Chords $ST$ , $SR$ and $TR$ are drawn in the circle. $QS$ is a tangent to the circle at $S$ .

	Use the diagram to prove the theorem which states that $Q\hat ST=\hat R$ .	$\textbf{[5]}$

Written on
November 2020 - Paper 2

Question 9.2

$9.2$	Chord $QN$ bisects $M\hat NP$ and intersects chord $MP$ at $S$ . The tangent at $P$ meets $MN$ produced at $R$ such that $QN\parallel PR$ . Let $\hat P_1=x$ .

$\:\: 9.2.1$	Determine the following angles in terms of $x$ . Give reasons
$\quad (a)$	$\hat N_2$	$(2)$
$\quad (b)$	$\hat Q_2$	$(2)$
$\:\: 9.2.2$	Prove, giving reasons, that $\frac{\displaystyle MN}{\displaystyle NR}=\frac{\displaystyle MS}{\displaystyle SQ}$	$(6)$
		$\textbf{[10]}$

Written on
November 2020 - Paper 2

Question 10

In the diagram, a circle passes through $D$ , $B$ and $E$ . Diameter $ED$ of the circle is produced to $C$ and $AC$ is a tangent to the circle at $B$ . $M$ is a point on $DE$ such that $AM\perp DE$ . $AM$ and chord $BE$ intersect at $F$ .

$10.1$	Prove, giving reasons, that:
$\quad 10.1.1$	$FBDM$ is a cyclic quadrilateral	$(3)$
$\quad 10.1.2$	$\hat B_3=\hat F_1$	$(4)$
$\quad 10.1.3$	$\Delta CDB\,\|\|\|\,\Delta CBE$	$(3)$
$10.2$	If it is further given that $CD=2$ units and $DE=6$ units, calculate the length of:
$10.2.1$	$BC$	$(3)$
$10.2.2$	$DB$	$(4)$
		$\textbf{[17]}$

2020-nov-p2

Question 1

Question 2

Question 3

Question 4

Question 5

Question 6

Question 7

Question 8.1

Question 8.2

Question 9.1

Question 9.2

Question 10