2020 Nov P2 Q6

Question 6

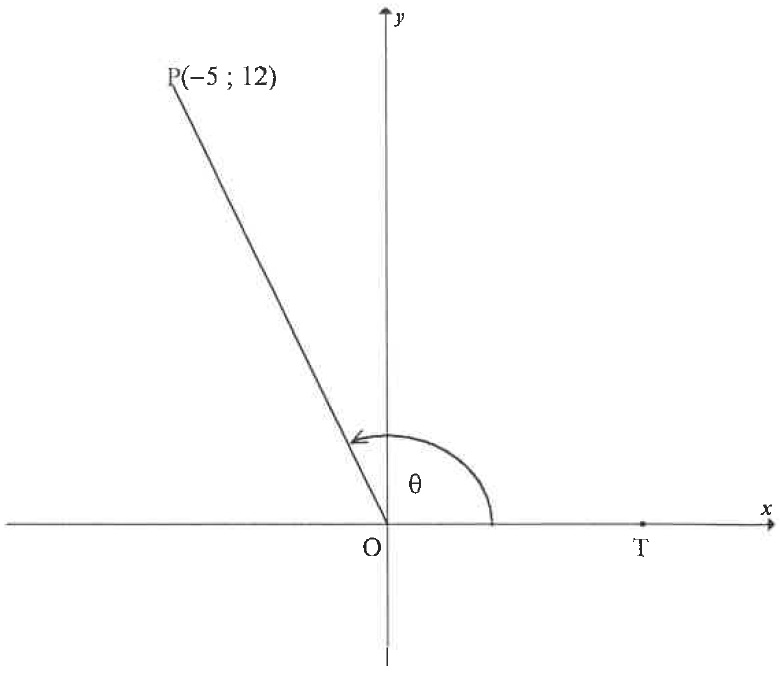
$6.1$	In the diagram, $P(-5\,;\,12)$ and $T$ lies on the positive $x$ -axis. $P\hat OT=\theta$

Answer the following without using a calculator:
$\quad 6.1.1$	Write down the value of $\tan\theta$	$(1)$
$\quad 6.1.2$	Calculate the value of $\cos\theta$	$(3)$
$\quad 6.1.3$	$S(a\,;\,b)$ is a point in the third quadrant such that $T\hat OS=\theta+90^{\circ}$ and $OS=6,5$ units. Calculate the value of $b$ .	$(4)$
$6.2$	Determine, without using a calculator, the value of the following trigonometric expression: $\frac{\displaystyle \sin{2x}.\cos(-x)+\cos{2x}.\sin(360^{\circ}-x)}{\displaystyle \sin(180^{\circ}+x)}$	$(5)$
$6.3$	Determine the general solution of the following equation: $6\sin^2 x+7\cos{x}-3=0$	$(6)$
$6.4$	Given: $x+\frac{\displaystyle 1}{\displaystyle x}=3\cos{A}$ and $x^2+\frac{\displaystyle 1}{\displaystyle x^2}=2$ Determine the value of $\cos{2A}$ without using a calculator.	$(5)$
		$\textbf{[24]}$