2020 Nov P2 Q10

Question 10

In the diagram, a circle passes through $D$ , $B$ and $E$ . Diameter $ED$ of the circle is produced to $C$ and $AC$ is a tangent to the circle at $B$ . $M$ is a point on $DE$ such that $AM\perp DE$ . $AM$ and chord $BE$ intersect at $F$ .

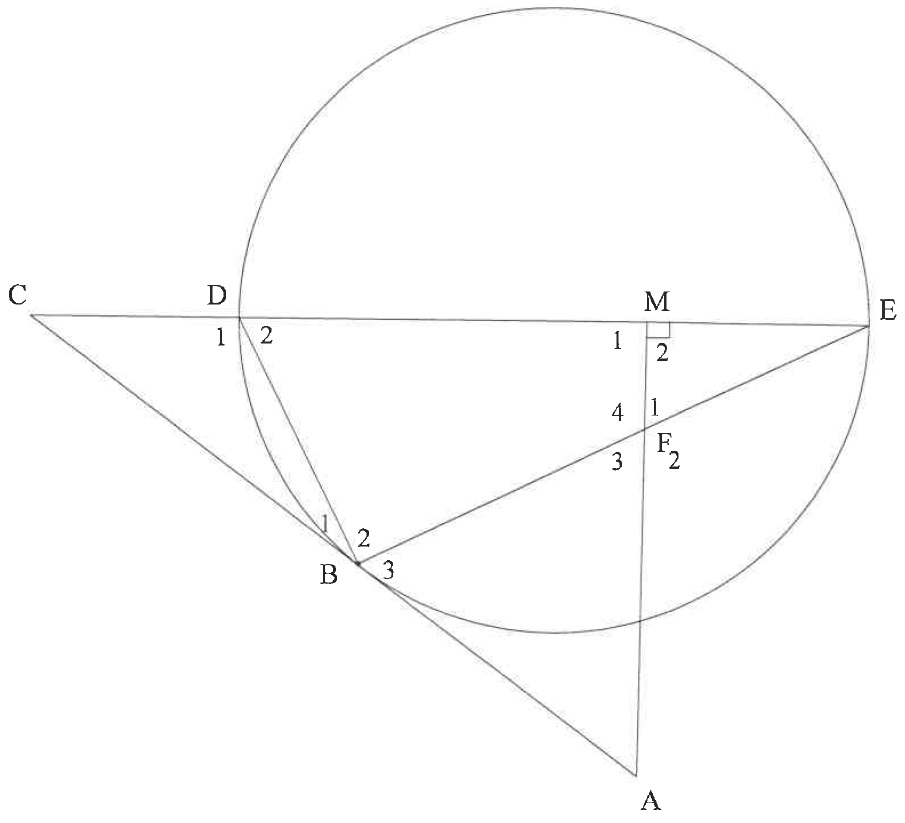$10.1$	Prove, giving reasons, that:
$\quad 10.1.1$	$FBDM$ is a cyclic quadrilateral	$(3)$
$\quad 10.1.2$	$\hat B_3=\hat F_1$	$(4)$
$\quad 10.1.3$	$\Delta CDB\,\|\|\|\,\Delta CBE$	$(3)$
$10.2$	If it is further given that $CD=2$ units and $DE=6$ units, calculate the length of:
$10.2.1$	$BC$	$(3)$
$10.2.2$	$DB$	$(4)$
		$\textbf{[17]}$