| 10.2 | In the diagram, ST and VT are tangents to the circle at S and V respectively. R is a point on the circle and W is a point on chord RS such that WT is parallel to RV. SV and WT are drawn. WT intersects SV at K. Let S^2=x. |
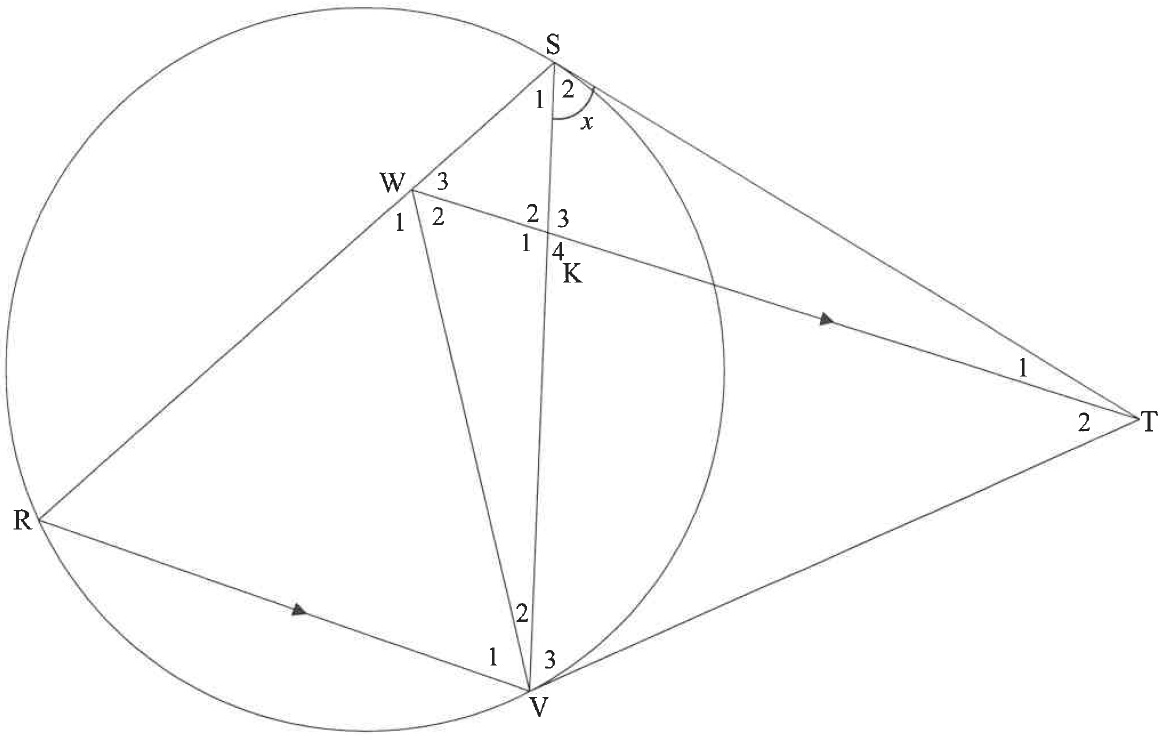 |
| 10.2.1 | Write down, with reasons, THREE other angles EACH equal to x. | (6) |
| 10.2.2 | Prove, with reasons, that: | |
| (a) | WSTV is a cyclic quadrilateral | (2) |
| (b) | ΔWRV is isosceles | (4) |
| (c) | ΔWRV∣∣∣ΔTSV | (3) |
| (d) | SRRV=TSKV | (4) |
| | [19] |