Home Tutors Exams

Probability

Written on
November 2020 - Paper 1

Question 10

In a certain country, $10$ -digit telephone numbers with the following format were introduced:

Digits may be repeated.
$10.1$	How many possible $10$ -digit telephone numbers could be formed?	$(2)$
$10.2$	Certain restrictions were placed on the groups of digits: Area code: must be $3$ digits and the first digit can NOT be $0$ or $1$ Exchange code: must be $3$ digits and the first and second digits can NOT be $0$ or $1$ Number: must be $4$ digits and the first digit MUST be a $0$ or $1$
$\quad 10.2.1$	How many valid $10$ -digit telephone numbers could be formed by applying the given restrictions?	$(3)$
$\quad 10.2.2$	Determine the probability that any randomly chosen $10$ -digit telephone number would be a valid phone number.	$(2)$
		$\textbf{[7]}$

Written on
November 2019 - Paper 1

Question 10

The school library is open from Monday to Thursday. Anna and Ben both studied in the school library one day this week. If the chance of studying any day in the week is equally likely, calculate the probability that Anna and Ben studied on:
$10.1$	The same day	$(2)$
$10.2$	Consecutive days	$(3)$
		$\textbf{[5]}$

Written on
November 2020 - Paper 1

Question 11

Harry shoots at a target board. He has a $50\%$ chance of hitting the bull's eye on each shot.
$11.1$	Calculate the probability that Harry will hit the bull's eye in his first shot and his second shot.	$(2)$
$11.2$	Calculate the probability that Harry will hit the bull's eye at least twice in his first three shots.	$(3)$
$11.3$	Glenda also has a $50\%$ chance of hitting the bull's eye on each shot. Harry and Glenda will take turns to shoot an arrow and the first person to hit the bull's eye will be the winner. Calculate the probability that the person who shoots first will be the winner of the challenge.	$(3)$
		$\textbf{[8]}$

Written on
November 2019 - Paper 1

Question 11

$11.1$	Events $A$ and $B$ are independent. $P(A)=0,4$ and $P(B)=0,25$ .
$\quad 11.1.1$	Represent the given information on a Venn diagram. Indicate on the Venn diagram the probabilities associated with each region.	$(3)$
$\quad 11.1.2$	Determine $P(A\; or\; NOT\; B)$ .	$(2)$
$11.2$	Motors Incorporated manufacture cars with $5$ different body styles, $4$ different interior colours and $6$ different exterior colours, as indicated in the table below.

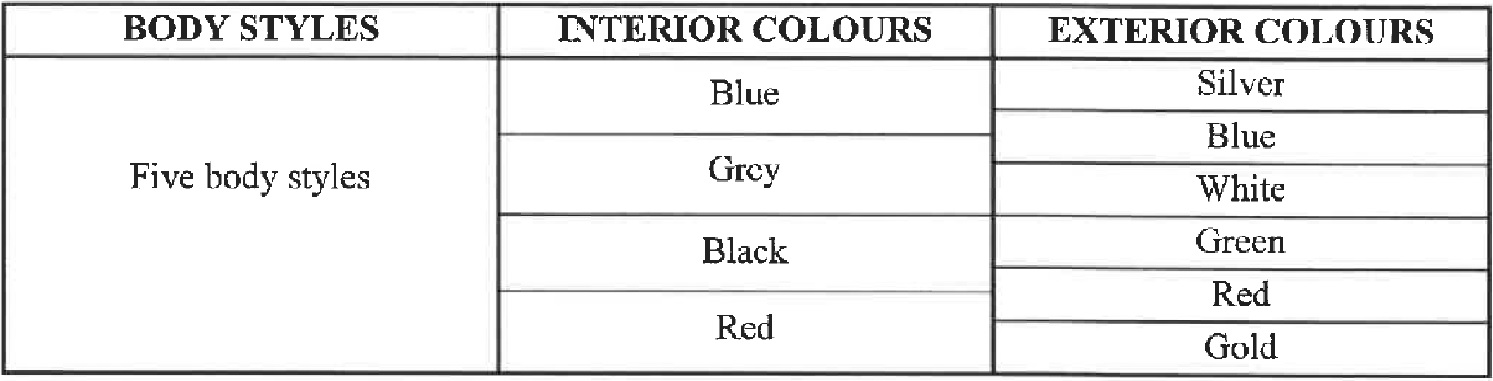	The interior colour of the car must NOT be the same as the exterior colour. Motors Incorporated wants to display one of each possible variation of its car in their showroom. The showroom has a floor space of $500\, m^2$ and each car requires a floor space of $5\, m^2$ .
	Is this display possible? Justify your answer with the necessary calculations.	$(6)$
		$\textbf{[11]}$

← Back to the exams