2019 Nov P1 Q4

Question 4

$4.1$	Given: $h(x)=\frac{\displaystyle -3}{\displaystyle x-1}+2$
$\quad 4.1.1$	Write down the equations of the asymptotes of $h$ .	$(2)$
$\quad 4.1.2$	Determine the equation of the axis of symmetry of $h$ that has a negative gradient.	$(2)$
$\quad 4.1.3$	Sketch the graph of $h$ , showing the asymptotes and the intercepts with the axes.	$(4)$
$4.2$	The graphs of $\: f(x)=\frac{\displaystyle 1}{\displaystyle 2}(x+5)^2-8$ and $\: g(x)=\frac{\displaystyle 1}{\displaystyle 2}x+\frac{\displaystyle 9}{\displaystyle 2}$ are sketched below. $A$ is the turning point of $f$ . The axis of symmetry of $f$ intersects the $x$ -axis at $E$ and the line $g$ at $D(m\,;\,n)$ . $C$ is the $y$ -intercept of $f$ and $g$ .

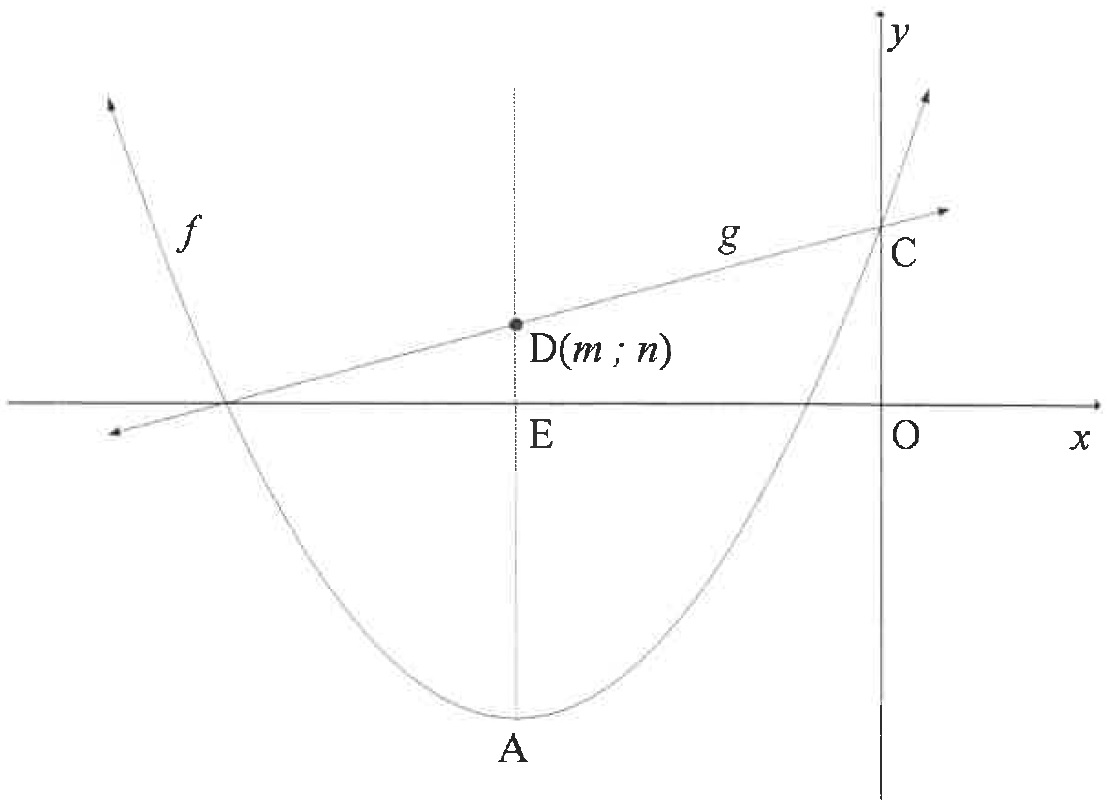$\quad 4.2.1$	Write down the coordinates of $A$ .	$(2)$
$\quad 4.2.2$	Write down the range of $f$ .	$(1)$
$\quad 4.2.3$	Calculate the values of $m$ and $n$ .	$(3)$
$\quad 4.2.4$	Calculate the area of $OCDE$ .	$(3)$
$\quad 4.2.5$	Determine the equation of $g^{-1}$ , the inverse of $g$ , in the form $y=...$	$(2)$
$\quad 4.2.6$	If $h(x)=g^{-1}(x)+k \:$ is a tangent to $f$ , determine the coordinates of the point of contact between $h$ and $f$ .	$(4)$
		$\textbf{[23]}$

Below are the graphs of $\: f(x)=x^2+bx-3$ and $\: g(x)=\frac{\displaystyle a}{\displaystyle x+p}$ . $f$ has a turning point at $C$ and passes through the $x$ -axis at $(1\;;\,0)$ . $D$ is the $y$ -intercept of both $f$ and $g$ . The graphs $f$ and $g$ also intersect each other at $E$ and $J$ . The vertical asymptote of $g$ passes through the $x$ -intercept of $f$ .

$4.1$	Write down the value of $p$ .	$(1)$
$4.2$	Show that $a=3$ and $b=2$ .	$(3)$
$4.3$	Calculate the coordinates of $C$ .	$(4)$
$4.4$	Write down the range of $f$ .	$(2)$
$4.5$	Determine the equation of the line through $C$ that makes an angle of $45^\circ$ with the positive $x$ -axis. Write your answer in the form $y=...$	$(3)$
$4.6$	Is the straight line, determined in QUESTION $4.5$ , a tangent to $f$ ? Explain your answer.	$(2)$
$4.7$	The function $h(x)=f(m-x)+q$ has only one $x$ -intercept at $x=0$ . Determine the values of $m$ and $q$ .	$(4)$
		$\textbf{[19]}$