Home Tutors Exams

Calculus

Written on
November 2020 - Paper 1

Question 7

$7.1$	Determine $f^\prime (x)$ from first principles if $f(x)=2x^2-1$ .	$(5)$
$7.2$	Determine:
$\quad 7.2.1$	$\frac{\displaystyle d}{\displaystyle dx}(\sqrt[5]{x^2}+x^3)$	$(3)$
$\quad 7.2.2$	$f^\prime (x)$ if $f(x)=\frac{\displaystyle 4x^2-9}{\displaystyle 4x+6}\:$ ; $x\neq -\frac{\displaystyle 3}{\displaystyle 2}$	$(4)$
		$\textbf{[12]}$

Written on
November 2019 - Paper 1

Question 7

$7.1$	Determine $f^\prime (x)$ from first principles if it is given that $f(x)=4-7x$ .	$(4)$
$7.2$	Determine $\frac{\displaystyle dy}{\displaystyle dx}$ if $y=4x^8+\sqrt{x^3}$	$(3)$
$7.3$	Given: $y=ax^2+a$ Determine:
$\quad 7.3.1$	$\frac{\displaystyle dy}{\displaystyle dx}$	$(1)$
$\quad 7.3.2$	$\frac{\displaystyle dy}{\displaystyle da}$	$(2)$
$7.4$	The curve with the equation $y=x+\frac{\displaystyle 12}{\displaystyle x}$ passes through the point $A(2\; ;\, b)$ . Determine the equation of the line perpendicular to the tangent to the curve at $A$ .	$(4)$
		$\textbf{[14]}$

Written on
November 2020 - Paper 1

Question 8

The graph of $g(x)=ax^3+bx^2+cx$ , a cubic function having a $y$ -intercept of $0$ , is drawn below. The $x$ -coordinates of the turning points of $g$ are $-1$ and $2$ .

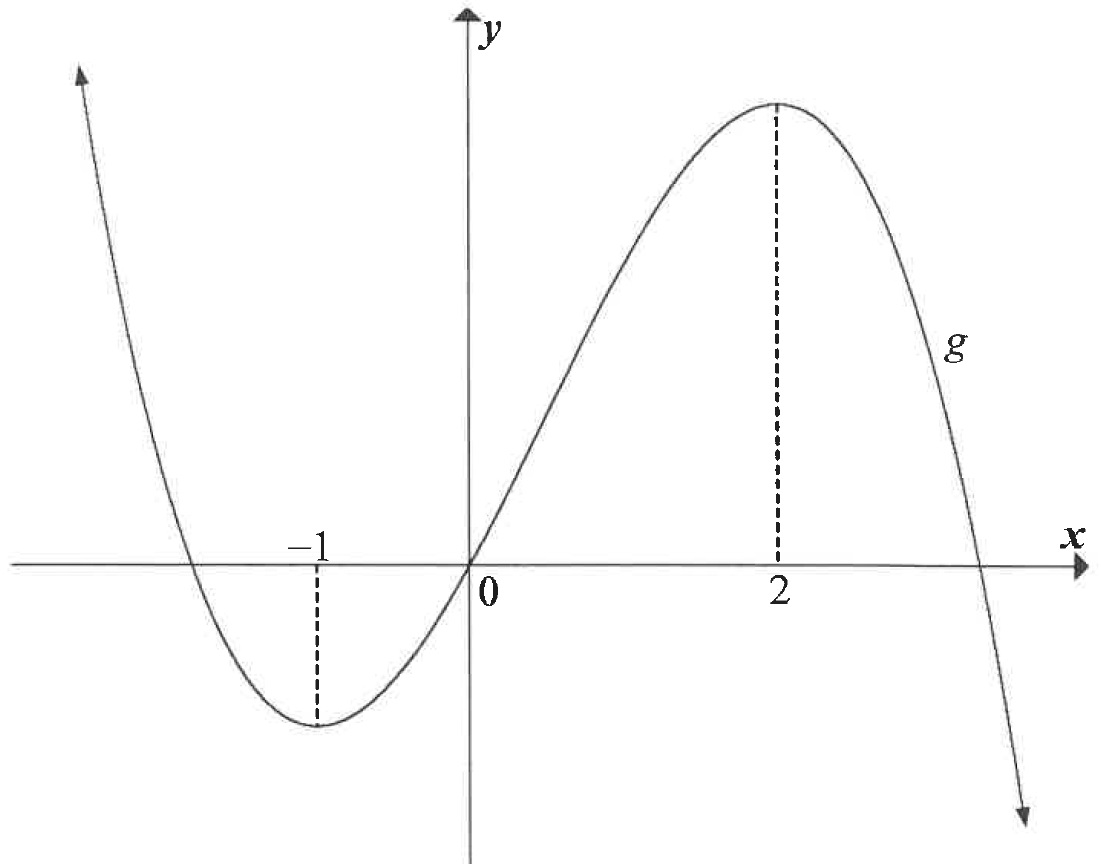$8.1$	For which values of $x$ will $g$ increase?	$(2)$
$8.2$	Write down the $x$ -coordinate of the point of inflection of $g$ .	$(2)$
$8.3$	For which values of $x$ will $g$ be concave down?	$(2)$
$8.4$	If $g^\prime (x)=-6x^2+6x+12\,$ , determine the equation of $g$ .	$(4)$
$8.5$	Determine the equation of the tangent to $g$ that has the maximum gradient. Write your answer in the form $y=mx+c\,$ .	$(5)$
		$\textbf{[15]}$

Written on
November 2019 - Paper 1

Question 8

After flying a short distance, an insect came to rest on a wall. Thereafter the insect started crawling on the wall. The path that the insect crawled can be described by $h(t)=(t-6)(-2t^2+3t-6)$ , where $h$ is the height (in cm) above the floor and $t$ is the time (in minutes) since the insect started crawling.
$8.1$	At what height above the floor did the insect start to crawl?	$(1)$
$8.2$	How many times did the insect reach the floor?	$(3)$
$8.3$	Determine the maximum height that the insect reached above the floor.	$(4)$
		$\textbf{[8]}$

Written on
November 2020 - Paper 1

Question 9

A closed rectangular box has to be constructed as follows: Dimensions: length $(l)$ , width $(w)$ and height $(h)$ . The length $(l)$ of the base has to be $3$ times its width $(w)$ . The volume has to be $5\,m^3$ . The material for the top and the bottom parts costs $R15$ per square metre and the material for the sides costs $R6$ per square metre.
$9.1$	Show that the cost to construct the box can be calculated by: $Cost=90w^2+48wh$	$(4)$
$9.2$	Determine the width of the box such that the cost to build the box is a minimum.	$(6)$
		$\textbf{[10]}$

Written on
November 2019 - Paper 1

Question 9

Given: $f(x)=3x^3$
$9.1$	Solve $f(x)=f^\prime (x)$	$(3)$
$9.2$	The graphs $f$ , $f^\prime$ and $f^{\prime \prime}$ all pass through the point $(0\; ; \,0)$ .
$\quad 9.2.1$	For which of the graphs will $(0\; ; \,0)$ be a stationary point?	$(1)$
$\quad 9.2.2$	Explain the difference, if any, in the stationary points referred to in QUESTION $9.2.1$ .	$(2)$
$9.3$	Determine the vertical distance between the graphs of $f^\prime$ and $f^{\prime \prime}$ at $x=1$ .	$(3)$
$9.4$	For which value(s) of $x$ is $f(x)-f^\prime (x)<0$ ?	$(4)$
		$\textbf{[13]}$

← Back to the exams