Funatic Maths

2020-nov-p1

  • Written on
    - Paper 1

    Question 1

    1.11.1 Solve for xx:
    1.1.1\quad 1.1.1 x2−6x=0x^2-6x=0 (2)(2)
    1.1.2\quad 1.1.2 x2+10x+8=0x^2+10x+8=0\quad (correct to TWO decimal places) (3)(3)
    1.1.3\quad 1.1.3 (1−x)(x+2)<0(1-x)(x+2)<0 (3)(3)
    1.1.4\quad 1.1.4 x+18=x−2\sqrt{x+18}=x-2 (5)(5)
    1.21.2 Solve simultaneously for xx and yy:
    x+y=3  x+y=3\; and   2x2+4xy−y=15\;2x^2+4xy-y=15    		 (6)(6)
    1.31.3 If nn is the largest integer for which n200<5300n^{200}<5^{300}, determine the value of nn. (3)(3)
    [22]\textbf{[22]}

  • Written on
    - Paper 1

    Question 2

    2.12.1 7 ;x ;y ;−11 ;...7 \,; x \,; y \,; -11 \,; ... is an arithmetic sequence. Determine the values of xx and yy. (4)(4)
    2.22.2 Given the quadratic number pattern:  −3 ;6 ;27 ;60 ;...\, -3 \,; 6 \,; 27 \,; 60 \,; ...
    2.2.1\quad 2.2.1 Determine the general term of the pattern in the form  Tn=an2+bn+c\:T_n=an^2+bn+c. (4)(4)
    2.2.2\quad 2.2.2 Calculate the value of the 50th50^{th} term of the pattern. (2)(2)
    2.2.3\quad 2.2.3 Show that the sum of the first nn first-differences of this pattern can be given by  Sn=6n2+3n\:S_n=6n^2+3n . (3)(3)
    2.2.4\quad 2.2.4 How many consecutive first-differences were added to the first term of the quadratic number pattern to obtain a term in the quadratic number pattern that has a value of 21 06021\,060? (4)(4)
    [17]\textbf{[17]}

  • Written on
    - Paper 1

    Question 3

    3.13.1 Prove that  ∑k=1∞4.32−k\: \sum\limits_{k=1}^{\infty} 4.3^{2-k} is a convergent geometric series. Show ALL your calculations. (3)(3)
    3.23.2 If  ∑k=p∞4.32−k=29\: \sum\limits_{k=p}^{\infty} 4.3^{2-k}=\frac{\displaystyle 2}{\displaystyle 9}, determine the value of pp. (5)(5)
    [8]\textbf{[8]}

  • Written on
    - Paper 1

    Question 4

    4.14.1 Given: h(x)=−3x−1+2h(x)=\frac{\displaystyle -3}{\displaystyle x-1}+2
    4.1.1\quad 4.1.1 Write down the equations of the asymptotes of hh. (2)(2)
    4.1.2\quad 4.1.2 Determine the equation of the axis of symmetry of hh that has a negative gradient. (2)(2)
    4.1.3\quad 4.1.3 Sketch the graph of hh, showing the asymptotes and the intercepts with the axes. (4)(4)
    4.24.2 The graphs of  f(x)=12(x+5)2−8\: f(x)=\frac{\displaystyle 1}{\displaystyle 2}(x+5)^2-8 and  g(x)=12x+92\: g(x)=\frac{\displaystyle 1}{\displaystyle 2}x+\frac{\displaystyle 9}{\displaystyle 2} are sketched below.
    • AA is the turning point of ff.
    • The axis of symmetry of ff intersects the xx-axis at EE and the line gg at D(m ; n)D(m\,;\,n).
    • CC is the yy-intercept of ff and gg.
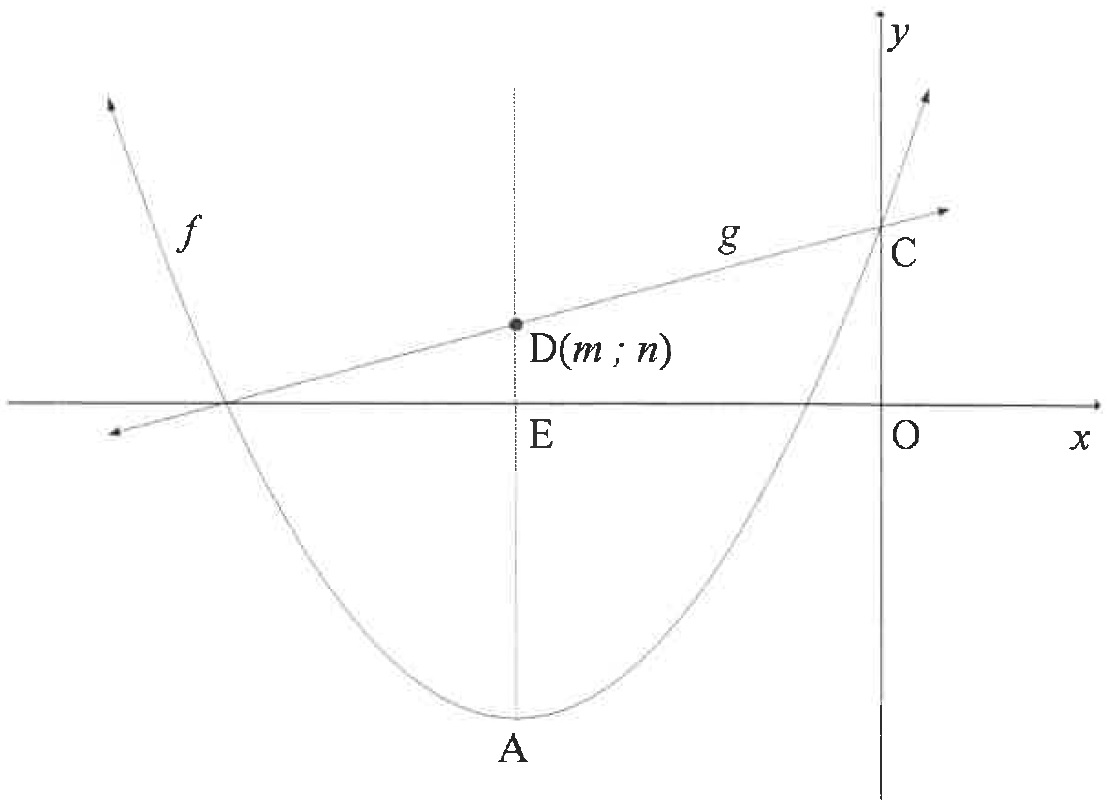    Image
    4.2.1\quad 4.2.1 Write down the coordinates of AA. (2)(2)
    4.2.2\quad 4.2.2 Write down the range of ff. (1)(1)
    4.2.3\quad 4.2.3 Calculate the values of mm and nn. (3)(3)
    4.2.4\quad 4.2.4 Calculate the area of OCDEOCDE. (3)(3)
    4.2.5\quad 4.2.5 Determine the equation of g−1g^{-1}, the inverse of gg, in the form y=...y=... (2)(2)
    4.2.6\quad 4.2.6 If h(x)=g−1(x)+k h(x)=g^{-1}(x)+k \: is a tangent to ff, determine the coordinates of the point of contact between hh and ff. (4)(4)
    [23]\textbf{[23]}

  • Written on
    - Paper 1

    Question 5

    The graph of  f(x)=3−x \,f(x)=3^{-x}\, is sketched below. AA is the yy-intercept of ff. BB is the point of intersection of ff and the line y=9y=9.
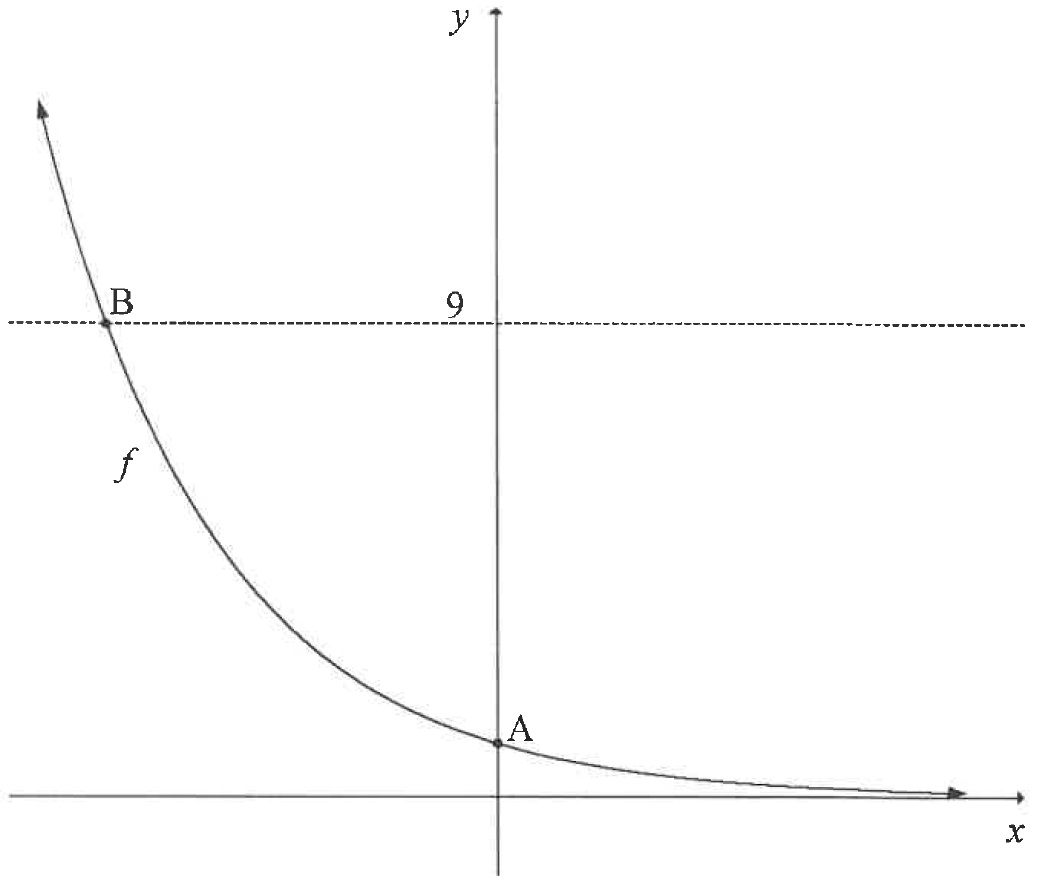    Image
    5.15.1 Write down the coordinates of AA. (1)(1)
    5.25.2 Determine the coordinates of BB. (3)(3)
    5.35.3 Write down the domain of f−1f^{-1}. (2)(2)
    5.45.4 Describe the translation from ff to h(x)=273xh(x)=\frac{\displaystyle 27}{\displaystyle 3^x}. (3)(3)
    5.55.5 Determine the values of xx for which h(x)<1h(x)<1. (3)(3)
    [12]\textbf{[12]}

  • Written on
    - Paper 1

    Question 6

    6.16.1 On 3131 January 20202020, Tshepo made the first of his monthly deposits of R1 000R1\,000 into a savings account. He continues to make monthly deposits of R1 000R1\,000 at the end of each month up until 3131 January 20322032. The interest rate was fixed at 7,5%7,5\% p.a., compounded monthly.
    6.1.1\quad 6.1.1 What will the investment be worth immediately after the last deposit? (4)(4)
    6.1.2\quad 6.1.2 If he makes no further payments but leaves the money in the account, how much money will be in the account on 3131 January 20332033? (2)(2)
    6.26.2 Jim bought a new car for R250 000R250\,000. The value of the car depreciated at a rate of 22%22\% p.a. annually according to the reducing-balance method. After how many years will its book value be R92 537,64R92\,537,64? (3)(3)
    6.36.3 Mpho is granted a loan under the following conditions:
    • The interest rate is 11,3%11,3\% p.a., compounded monthly.
    • The period of the loan is 66 years.
    • The monthly repayment on the loan is R1 500R1\,500.
    • Her first repayment is made one month after the loan is granted.
    6.3.1\quad 6.3.1 Calculate the value of the loan. (3)(3)
    6.3.2\quad 6.3.2 How much interest will Mpho pay in total over the first 55 years? (4)(4)
    [16]\textbf{[16]}

  • Written on
    - Paper 1

    Question 7

    7.17.1 Determine f′(x)f^\prime (x) from first principles if f(x)=2x2−1f(x)=2x^2-1. (5)(5)
    7.27.2 Determine:
    7.2.1\quad 7.2.1 ddx(x25+x3)\frac{\displaystyle d}{\displaystyle dx}(\sqrt[5]{x^2}+x^3) (3)(3)
    7.2.2\quad 7.2.2 f′(x)f^\prime (x) if f(x)=4x2−94x+6 f(x)=\frac{\displaystyle 4x^2-9}{\displaystyle 4x+6}\: ; x≠−32x\neq -\frac{\displaystyle 3}{\displaystyle 2} (4)(4)
    [12]\textbf{[12]}

  • Written on
    - Paper 1

    Question 8

    The graph of g(x)=ax3+bx2+cxg(x)=ax^3+bx^2+cx, a cubic function having a yy-intercept of 00, is drawn below. The xx-coordinates of the turning points of gg are −1-1 and 22.
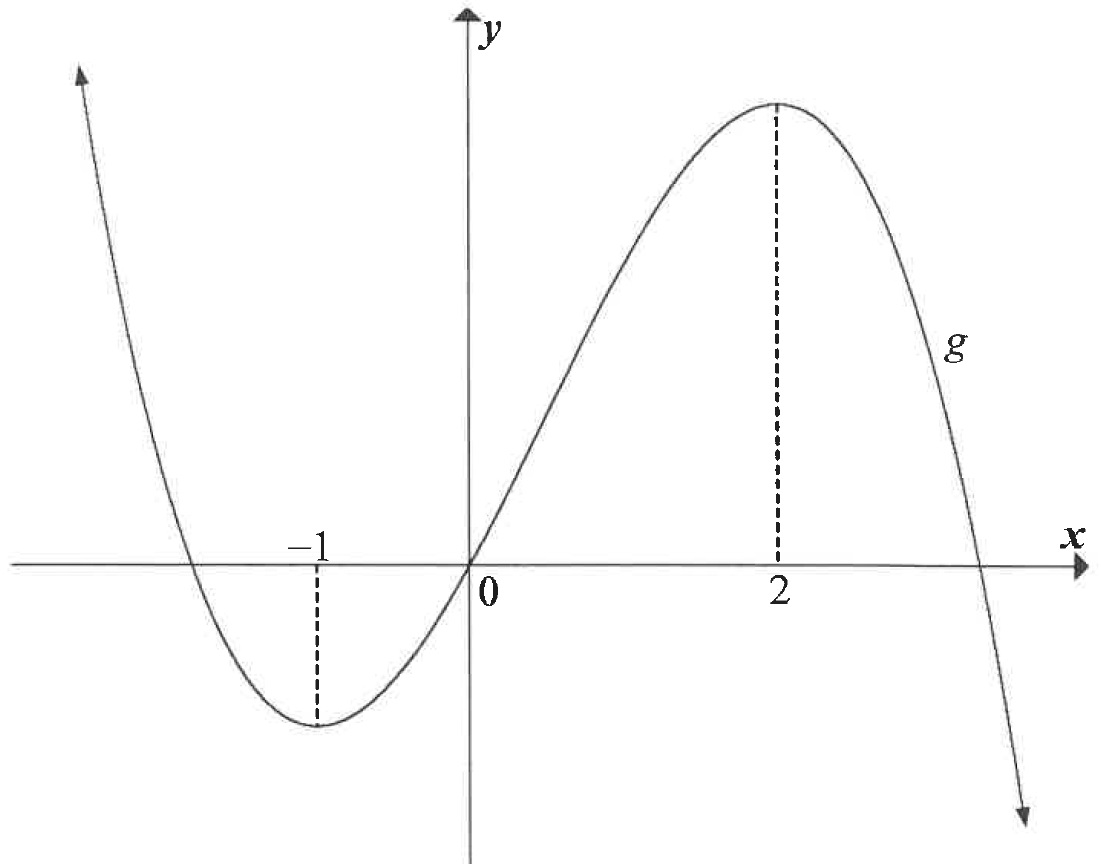    Image
    8.18.1 For which values of xx will gg increase? (2)(2)
    8.28.2 Write down the xx-coordinate of the point of inflection of gg. (2)(2)
    8.38.3 For which values of xx will gg be concave down? (2)(2)
    8.48.4 If g′(x)=−6x2+6x+12 g^\prime (x)=-6x^2+6x+12\,, determine the equation of gg. (4)(4)
    8.58.5 Determine the equation of the tangent to gg that has the maximum gradient. Write your answer in the form y=mx+c y=mx+c\,. (5)(5)
    [15]\textbf{[15]}

  • Written on
    - Paper 1

    Question 9

    A closed rectangular box has to be constructed as follows:
    • Dimensions: length (l)(l), width (w)(w) and height (h)(h).
    • The length (l)(l) of the base has to be 33 times its width (w)(w).
    • The volume has to be 5 m35\,m^3 .
    The material for the top and the bottom parts costs R15R15 per square metre and the material for the sides costs R6R6 per square metre.
    9.19.1 Show that the cost to construct the box can be calculated by: Cost=90w2+48whCost=90w^2+48wh (4)(4)
    9.29.2 Determine the width of the box such that the cost to build the box is a minimum. (6)(6)
    [10]\textbf{[10]}

  • Written on
    - Paper 1

    Question 10

    In a certain country, 1010-digit telephone numbers with the following format were introduced:
    Image
    Digits may be repeated.
    10.110.1 How many possible 1010-digit telephone numbers could be formed? (2)(2)
    10.210.2 Certain restrictions were placed on the groups of digits:
    • Area code: must be 33 digits and the first digit can NOT be 00 or 11
    • Exchange code: must be 33 digits and the first and second digits can NOT be 00 or 11
    • Number: must be 44 digits and the first digit MUST be a 00 or 11
    10.2.1\quad 10.2.1 How many valid 1010-digit telephone numbers could be formed by applying the given restrictions? (3)(3)
    10.2.2\quad 10.2.2 Determine the probability that any randomly chosen 1010-digit telephone number would be a valid phone number. (2)(2)
    [7]\textbf{[7]}

  • Written on
    - Paper 1

    Question 11

    Harry shoots at a target board. He has a 50%50\% chance of hitting the bull's eye on each shot.
    11.111.1 Calculate the probability that Harry will hit the bull's eye in his first shot and his second shot. (2)(2)
    11.211.2 Calculate the probability that Harry will hit the bull's eye at least twice in his first three shots. (3)(3)
    11.311.3 Glenda also has a 50%50\% chance of hitting the bull's eye on each shot. Harry and Glenda will take turns to shoot an arrow and the first person to hit the bull's eye will be the winner. Calculate the probability that the person who shoots first will be the winner of the challenge. (3)(3)
    [8]\textbf{[8]}
← Back to the exams