Funatic Maths

2019-nov-p1

  • Written on
    - Paper 1

    Question 1

    1.11.1 Solve for xx:
    1.1.1\quad 1.1.1 x2+5x−6=0x^2+5x-6=0 (3)(3)
    1.1.2\quad 1.1.2 4x2+3x−5=04x^2+3x-5=0\quad (correct to TWO decimal places) (3)(3)
    1.1.3\quad 1.1.3 4x2−1<04x^2-1<0 (3)(3)
    1.1.4\quad 1.1.4 (32+x)(32−x)=x(\sqrt{\sqrt{32}+x})(\sqrt{\sqrt{32}-x})=x (4)(4)
    1.21.2 Solve simultaneously for xx and yy:
    y+x=12  y+x=12\; and   xy=14−3x\;xy=14-3x    		 (5)(5)
    1.31.3 Consider the product 1×2×3×4×⋯×301 \times 2 \times 3 \times 4 \times \cdots \times 30.
    Determine the largest value of kk such that 3k3^k is a factor of this product.    		 (4)(4)
    [22]\textbf{[22]}

  • Written on
    - Paper 1

    Question 2

    2.12.1 Given the quadratic sequence:  321 ;290 ;261 ;234 ;...\:321 \,; 290 \,; 261 \,; 234 \,; ...
    2.1.1\quad 2.1.1 Write down the values of the next TWO terms of the sequence. (2)(2)
    2.1.2\quad 2.1.2 Determine the general term of the sequence in the form  Tn=an2+bn+c\:T_n=an^2+bn+c. (4)(4)
    2.1.3\quad 2.1.3 Which term(s) of the sequence will have a value of 7474? (4)(4)
    2.1.4\quad 2.1.4 Which term in the sequence has the least value? (2)(2)
    2.22.2 Given the geometric series:  58+516+532+...=K\, \frac{\displaystyle5}{\displaystyle8}+\frac{\displaystyle5}{\displaystyle16}+\frac{\displaystyle5}{\displaystyle32}+...=K
    2.2.1\quad 2.2.1 Determine the value of KK if the series has 2121 terms. (3)(3)
    2.2.2\quad 2.2.2 Determine the largest value of nn for which  Tn>58192\:T_n>\frac{\displaystyle5}{\displaystyle8192} (4)(4)
    [19]\textbf{[19]}

  • Written on
    - Paper 1

    Question 3

    3.13.1 Without using a calculator, determine the value of:  ∑y=3101y−2−∑y=3101y−1\: \sum\limits_{y=3}^{10}\frac{\displaystyle 1}{\displaystyle y-2} - \sum\limits_{y=3}^{10}\frac{\displaystyle 1}{\displaystyle y-1} (3)(3)
    3.23.2 A steel pavilion at a sports ground comprises of a series of 1212 steps, of which the first 33 are shown in the diagram below.
    Each step is 5 m5\,m wide. Each step has a rise of 13 m\frac{\displaystyle 1}{\displaystyle 3}\,m and has a tread of 23 m\frac{\displaystyle 2}{\displaystyle 3}\,m, as shown in the diagram below.
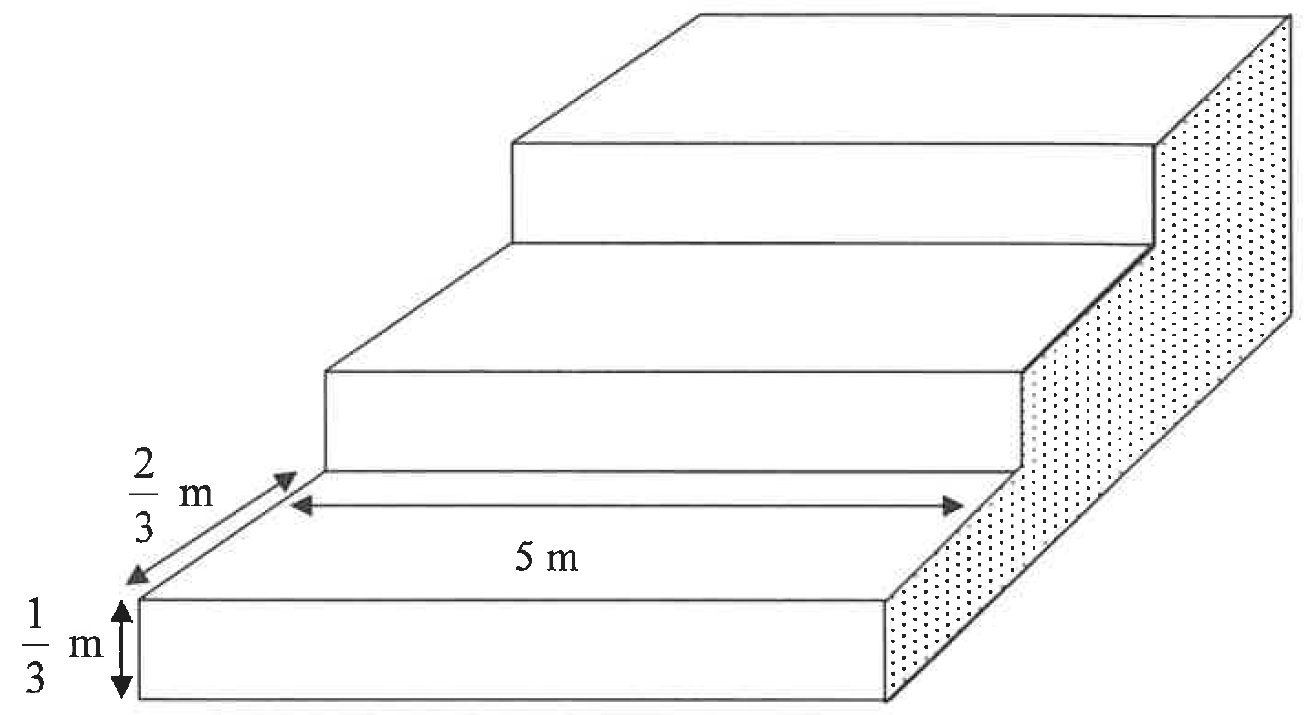    Image
    The open side (shaded on sketch) on each side of the pavilion must be covered with metal sheeting. Calculate the area (in m2m^2) of metal sheeting needed to cover both open sides. (6)(6)
    [9]\textbf{[9]}

  • Written on
    - Paper 1

    Question 4

    Below are the graphs of  f(x)=x2+bx−3\: f(x)=x^2+bx-3 and  g(x)=ax+p\: g(x)=\frac{\displaystyle a}{\displaystyle x+p}.
    • ff has a turning point at CC and passes through the xx-axis at (1  ; 0)(1\;;\,0).
    • DD is the yy-intercept of both ff and gg. The graphs ff and gg also intersect each other at EE and JJ.
    • The vertical asymptote of gg passes through the xx-intercept of ff.
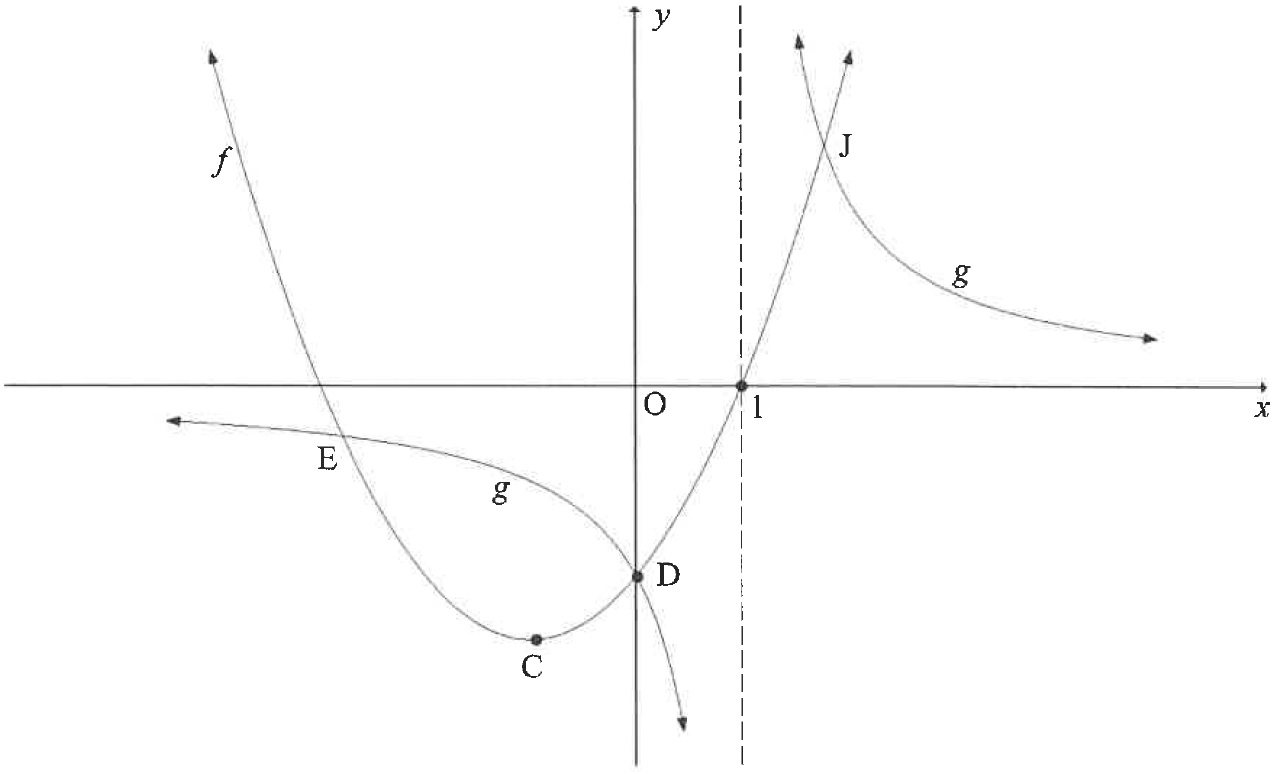    Image
    4.14.1 Write down the value of pp. (1)(1)
    4.24.2 Show that a=3a=3 and b=2b=2. (3)(3)
    4.34.3 Calculate the coordinates of CC. (4)(4)
    4.44.4 Write down the range of ff. (2)(2)
    4.54.5 Determine the equation of the line through CC that makes an angle of 45∘45^\circ with the positive xx-axis. Write your answer in the form y=...y=... (3)(3)
    4.64.6 Is the straight line, determined in QUESTION 4.54.5, a tangent to ff? Explain your answer. (2)(2)
    4.74.7 The function h(x)=f(m−x)+qh(x)=f(m-x)+q has only one xx-intercept at x=0x=0. Determine the values of mm and qq. (4)(4)
    [19]\textbf{[19]}

  • Written on
    - Paper 1

    Question 5

    Sketched below is the graph of  f(x)=kx ; k>0\,f(x)=k^x\,;\,k>0. The point (4  ; 16)(4\; ;\,16) lies on ff.
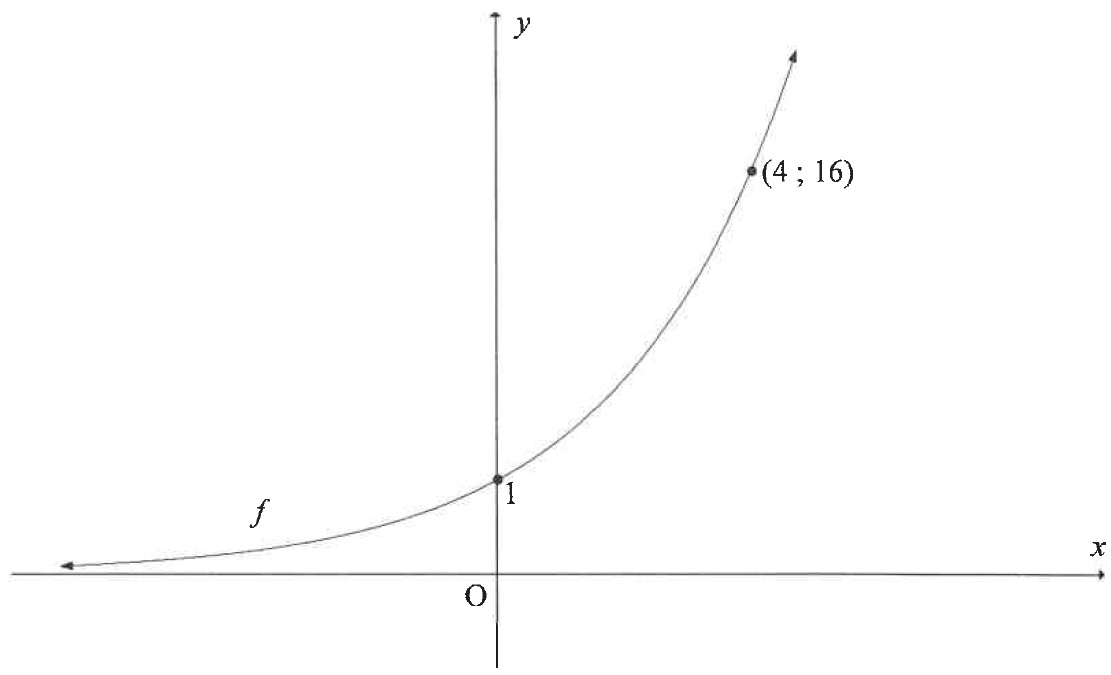    Image
    5.15.1 Determine the value of kk. (2)(2)
    5.25.2 Graph gg is obtained by reflecting graph ff about the line y=xy=x. Determine the equation of gg in the form y=...y=... (2)(2)
    5.35.3 Sketch the graph gg. Indicate on your graph the coordinates of two points on gg. (4)(4)
    5.45.4 Use your graph to determine the value(s) of xx for which:
    5.4.1\quad 5.4.1 f(x)×g(x)>0f(x) \times g(x)>0 (2)(2)
    5.4.2\quad 5.4.2 g(x)≤−1g(x) \leq -1 (2)(2)
    5.55.5 If h(x)=f(−x)h(x)=f(-x), calculate the value of xx for which f(x)−h(x)=154f(x)-h(x)=\frac{\displaystyle 15}{\displaystyle 4} (4)(4)
    [16]\textbf{[16]}

  • Written on
    - Paper 1

    Question 6

    6.16.1 Two friends, Kuda and Thabo, each want to invest R5 000R5\,000 for four years. Kuda invests his money in an account that pays simples interest at 8,3%8,3\% per annum. At the end of four years, he will receive a bonus of exactly 4%4\% of the accumulated amount. Thabo invests his money in an account that pays interest at 8%8\% p.a., compounded monthly.
    Whose investment will yield a better return at the end of four years? Justify your answer with appropriate calculations. (5)(5)
    6.26.2 Nine years ago, a bank granted Mandy a home loan of R525 000R525\,000. This loan was to be repaid over 2020 years at an interest rate of 10%10\% p.a., compounded monthly. Mandy's monthly repayments commenced exactly one month after the loan was granted.
    6.2.1\quad 6.2.1 Mandy decided to make monthly repayments of R6 000R6\,000 instead of the required R5 066,36R5\,066,36. How many payments will she make to settle the loan? (5)(5)
    6.2.2\quad 6.2.2 After making monthly repayments of R6 000R6\,000 for nine years, Mandy required money to fund her daughter's university fees. She approached the bank for another loan. Instead, the bank advised Mandy that the extra amount repaid every month could be regarded as an investment and that she could withdraw this full amount to fund her daughter's studies. Calculate the maximum amount that Mandy may withdraw from the loan account. (4)(4)
    [14]\textbf{[14]}

  • Written on
    - Paper 1

    Question 7

    7.17.1 Determine f′(x)f^\prime (x) from first principles if it is given that f(x)=4−7xf(x)=4-7x. (4)(4)
    7.27.2 Determine dydx\frac{\displaystyle dy}{\displaystyle dx} if y=4x8+x3y=4x^8+\sqrt{x^3} (3)(3)
    7.37.3 Given: y=ax2+ay=ax^2+a
    Determine:
    7.3.1\quad 7.3.1 dydx\frac{\displaystyle dy}{\displaystyle dx} (1)(1)
    7.3.2\quad 7.3.2 dyda\frac{\displaystyle dy}{\displaystyle da} (2)(2)
    7.47.4 The curve with the equation y=x+12xy=x+\frac{\displaystyle 12}{\displaystyle x} passes through the point A(2  ; b)A(2\; ;\, b). Determine the equation of the line perpendicular to the tangent to the curve at AA. (4)(4)
    [14]\textbf{[14]}

  • Written on
    - Paper 1

    Question 8

    After flying a short distance, an insect came to rest on a wall. Thereafter the insect started crawling on the wall. The path that the insect crawled can be described by h(t)=(t−6)(−2t2+3t−6)h(t)=(t-6)(-2t^2+3t-6), where hh is the height (in cm) above the floor and tt is the time (in minutes) since the insect started crawling.
    8.18.1 At what height above the floor did the insect start to crawl? (1)(1)
    8.28.2 How many times did the insect reach the floor? (3)(3)
    8.38.3 Determine the maximum height that the insect reached above the floor. (4)(4)
    [8]\textbf{[8]}

  • Written on
    - Paper 1

    Question 9

    Given: f(x)=3x3f(x)=3x^3
    9.19.1 Solve f(x)=f′(x)f(x)=f^\prime (x) (3)(3)
    9.29.2 The graphs ff, f′f^\prime and f′′f^{\prime \prime} all pass through the point (0  ; 0)(0\; ; \,0).
    9.2.1\quad 9.2.1 For which of the graphs will (0  ; 0)(0\; ; \,0) be a stationary point? (1)(1)
    9.2.2\quad 9.2.2 Explain the difference, if any, in the stationary points referred to in QUESTION 9.2.19.2.1. (2)(2)
    9.39.3 Determine the vertical distance between the graphs of f′f^\prime and f′′f^{\prime \prime} at x=1x=1. (3)(3)
    9.49.4 For which value(s) of xx is f(x)−f′(x)<0f(x)-f^\prime (x)<0? (4)(4)
    [13]\textbf{[13]}

  • Written on
    - Paper 1

    Question 10

    The school library is open from Monday to Thursday. Anna and Ben both studied in the school library one day this week. If the chance of studying any day in the week is equally likely, calculate the probability that Anna and Ben studied on:
    10.110.1 The same day (2)(2)
    10.210.2 Consecutive days (3)(3)
    [5]\textbf{[5]}

  • Written on
    - Paper 1

    Question 11

    11.111.1 Events AA and BB are independent. P(A)=0,4P(A)=0,4 and P(B)=0,25P(B)=0,25.
    11.1.1\quad 11.1.1 Represent the given information on a Venn diagram. Indicate on the Venn diagram the probabilities associated with each region. (3)(3)
    11.1.2\quad 11.1.2 Determine P(A  or  NOT  B)P(A\; or\; NOT\; B). (2)(2)
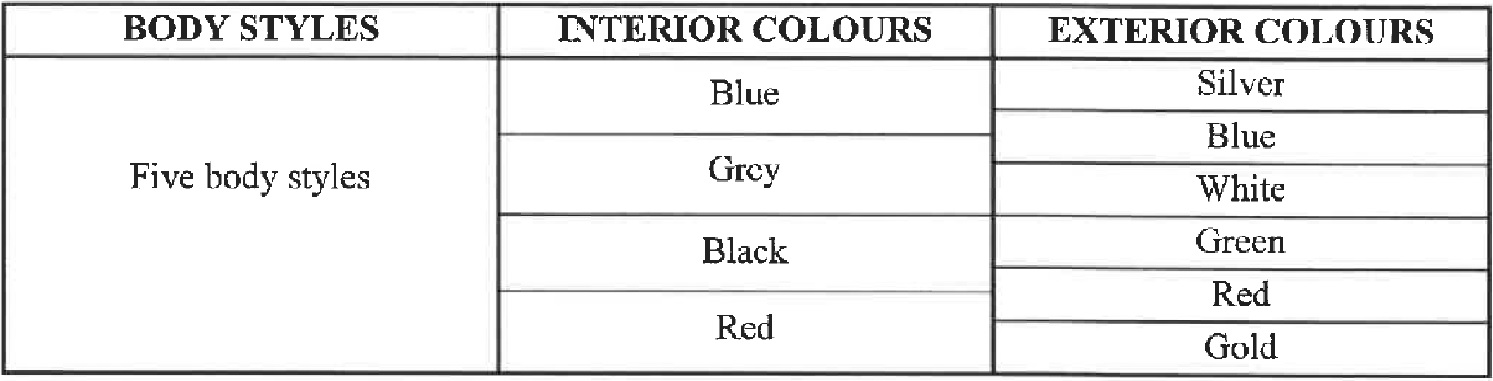
    11.211.2 Motors Incorporated manufacture cars with 55 different body styles, 44 different interior colours and 66 different exterior colours, as indicated in the table below.
    Image
    • The interior colour of the car must NOT be the same as the exterior colour.
    • Motors Incorporated wants to display one of each possible variation of its car in their showroom. The showroom has a floor space of 500 m2500\, m^2 and each car requires a floor space of 5 m25\, m^2.
    Is this display possible? Justify your answer with the necessary calculations. (6)(6)
    [11]\textbf{[11]}
← Back to the exams